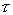Шипов Г.И. Теория физического вакуума

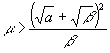
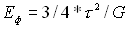
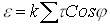
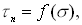
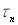
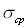
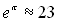
IMG SRC="Image58.gif" WIDTH=539 HEIGHT=228 >

Глава 1 Нерешенные проблемы современной теоретической физики 1.1. Проблема сил инерции в классической механике Проблема сил и полей инерции в классической механике и в других разделах физики является одной из запутанных. Лело в том, что си- лы инерции не удовлетворяют третьему закону Ньютона [13], поэто- му возникают трудности в разделении их на внешние и внутренние по отношению к изолированной системе, Наши знания об этих си- лах почти не изменились со времен И. Ньютона. В знаменитой книге А. Пайса " Научная деятельность и жизнь Альберта Эйнштейна", ав- тор замечает: " По моему мнению, проблема происхождения инерции была и остается наиболее темным вопросом в теории частиц и полей [14]». В нашей стране дискуссии по проблеме сил инерции периодически возникают через 20-30 лет. Основные вопросы, которые при этом обсуждаются, следующие: реальны ли силы инерции; что является их источником; являются ли они внешними или внутренними силами по отношению к изолированной механической системе. Анализ учебников по теоретической механике показывает отсут- ствие единого мнения по втим вопросам. Например,.-по вопросу ре- альны или нереальны силы инерции мнения распределяются (при- близительно) следующим образом: 60% авторов считает, что силы инерции нереальны [15]; 20% что они реальны [16]; 10% что часть сил инерции реальна, & часть нереальна; 10% авторов вообще обходят атот вопрос. Силы инерции наблюдаются в ускоренных системах отсчета, по- этому И. Ньютон, Л. Эйлер, Э, Мах, А. Эйнштейн и многие другие исследователи рассматривали эти силы как реальные. Из опыта так же следует, что при ускоренном движении в протя- женном теле возникает поле сил инерции, равнодействующая кото- рых приложена (иногда) к центру масс данного тела. Поэтому це- лесообразно поставить вопрос об изучении физических свойств поля инерции, порождающего силы инерции. Полагаю, что вопрос о си- лах и тем более полях инерции выходит далеко за рамки не только механики Ньютона, но и классической механики вообще. В настоящее время в нерелятивистской механике ускоренных си- стем отсчета известны четыре типа сил инерции. Три силы инерции связаны с вращением в трехмерном пространстве, а именно: центро- бежная сила FI == -т[и[ит]}, (1.1) сила Кориолиса РЗ = -2m[(Jv], (1.2) и сила, связанная с вращательным ускорением, РЗ == -m[iJv]. (1.3) Четвертая сила инерции F, 4 -mW (1.4) возникает при поступательном ускорении W тела и также связана с вращением в пространственно-временных плоскостях, повтому еди- ное описание всех сил инерции требует релятивистского подхода [17]. Мы уже отметили, что силы инерции вызваны полями инерции, поэтому проблема сил инерции в классической механике не может быть успешно решена без исследования такого важного вопроса как динамика полей инерции. Эту проблему не решает и общая теория относительности, пред- ложенная А. Эйнштейном. Он считал [18], что геометрия на вращаю- щемся диске изменяется и вместо евклидовой становится геометрией поверхности отрицательной кривизны в трехмерном евклидовом про- странстве. Из формул (1.1)-( 1.3) видно, что всякое вращение материи вызывает в ней Действие сил инерции. Кроме того, вращение пред- ставляет собой движение в угловых координатах (например, в углах Эйлера). Поэтому представления Эйнштейна о вращении не явля- ются полными, так как римаиова геометрия не учитывает движение в неголономных координатах yi,ya, рз> описывающих реальное (а не координатное, как у Эйнштейна) вращение. Общая теория относительности Эйнштейна, специальная теория относительности и относительность Галилея-Ньютона представляют собой класс теорий, в основу которых положена поступательная от- носительность. В таких теориях рассматривают преобразования го- лоиомных поступательных (или трансляционных) координат. В нере- лятивистской физике ето преобразования координат х,у, г, а в реля- тивистской соответственно а:1,»3, ж3 и ас° = ct. Однако при описании вращательного движения к преобразованиям трансляционных коор- динат необходимо добавлять преобразования угловых (или враща- тельных) координат. Поэтому полное описание сил инерции требует расширения теории относительности путем включения в нее теории вращательной относительности. 1.2. Неголономные координаты Известно, что в классической механике произвольно ускоренная система отсчета имеет шесть степеней свободы, поэтому взаимное положение трехмерных ускоренных систем задается шестью коорди- натами: тремя трансляционными координатами х\,х^,хз , задающи- ми положения начала О системы отсчета и тремя углами Эйлера yi,V7,2i Уз • Геометрия такого шестимерного многообразия должна отличать- ся от евклидовой геометрии механики Ньютона тем, что координаты а-1, д-2?хз образуют полярный вектор, а координаты y?i, у2»Уз не обра- зуют вектора вообще. Вектор (аксиальный) образуют бесконечно малые приращения углов dipi, dyy, dys • В общем случае полярный и аксиальный векторы имеют различ- ные законы преобразования; если любая из координат полярного век- тора является скаляром, то координаты аксиального вектора явля- ются пс ев до скалярами. Это означает, что аксиальный вектор при поворотах преобразуется как полярный вектор при трансляциях, т.е. знак проекций этого вектора на координатные оси не меняется; при дискретном преобразовании, соответствующем инверсии координат- ных осей, проекции аксиального вектора не меняют своего знака, в то время как проекции полярного вектора меняют знак. Координаты ^1,^21^3 с указанными свойствами называются не- голономными координатами (матрицы преобразования поворотов на конечный угол не коммутируют друг с другом) в отличие от голо- номных координат Х1,х-г,хз • При движении в неголономных коорди- натах результат двух поворотов на конечные углы, вообще говоря, зависит от последовательности втих поворотов. Лля иллюстрации этого утверждения, рассмотрим два последовательных поворота во- а б в 90' х х Рис. 1.2: Смена порядка последовательных поворотов на угол 180°: а - поворот на 90° по часовой стрелке вокруг оси х, б - то же вокруг оси z, в - результат двух последовательных поворотов круг осей х и z на утлы 90°, рис. 1.1, 1.2. Из рисунков видно, что результат двух конечных поворотов во- круг осей х и z зависит от последовательности этих поворотов (по- ложение квадрата со звездочкой в верхнем правом углу на рис. 1.1.в и рис.1.2.в не совпадают). Аксиальные вектора различаются ориентацией и для их полного описания необходимо задавать ориентируемые многообразия, харак- теризуемые правыми и левыми системами отсчета. В ориентируе- мых многообразиях появляются правые и левые аксиальные вектора и всякий нулевой аксиальный вектор можно представить как пару аксиальных векторов, проекции которых различаются знаками. Примером аксиального вектора является трехмерная угловая ско- рость и, входящая в уравнения Эйлера (1.6). Этот вектор преобра- зуется не только в группе Галилея-Ньютона (1-7), но и в группе трех- мерных вращении 0(3), действующей на многообразии угловых ко- ординат ^уз.Уз- Если теперь мы захотели бы построить теорию относительности, совмещающую поступательную относительность Галилея-Ньютона с вращательной относительностью, нам необходимо было бы расши- рить наши представления о геометрии пространства событий такой теории. 1.3. Вращательная относительность и гео- метрия, которая ей соответствует Геометрия Евклида, лежащая в основе классической механики, представляет собой трехмерное точечное многообразие. Для того, чтобы учесть вращ&тельные степени свободы произвольно ускорен- ной трехмерной системы отсчета, нам необходимо использовать ше- стимерное многообразие или трехмерное многообразие ориентируе- мых точек [I9]. Под трехмерной ориентируемой точкой подразумева- ется точка, снабженная ортогональным репером. Простейшим обобщением трехмерной геометрии Евклида на слу- чай, когда все точки многообразия ориентируемые, является геоме- трия абсолютного параллелизма [20-22] (см. также Часть 2), постро- енная на шестимерном многообразии координат ^1,ху,хз,У1,у'2,Уз . Это многообразие удобно представить как векторное расслоение с базой» образованной многообразием трансляционных координат a"i | •С2» •Яз и слоем, заданным в каждой точке Ха (а = 1,2,3) ортонорми- рованными реперами ел, А ==1,2.3 (1.8) где символ Л нумерует вектора репера. Фактически любой из репе- ров ел является математическим образом трехмерной произвольно ускоренной системы отсчета. Согласно теореме Эйлера, бесконечно малые повороты вокруг трех осей репера (1.8) можно заменить одним поворотом на, угол dx вокруг определенной оси, проходящей через нач&ло репера О. Бес- конечно малый поворот (в отличие от конечного поворота) можно задать вектором 4t=rfxex , (1.9) где вектор е^ направлен вдоль мгновенной оси вращения системы отсчета. Это направление выбирается так, что если смотреть с конца вектора е^ на неподвижную точку О, то поворот совершается против часовой стрелки (правая система отсчета). Бесконечно малое изменение векторов репера е^ при повороте d\ ииеет вид Дел = [dxe^l. (1.10) Если разделить (1.10) на dt^ то мы получим <и»л ,dX . , . -а-=[ул]=[^ел], (1.11) где и = dx/tft - трехмерная угловая скорость вращения системы от- счета относительно мгновенной оси. Выбирая ортогональный репер (1.12) «) 6) ^„«•в = ^в 1 А=В О Ai-B ' Л Л с» S ! 01=0 «Ул=^=^0 »+» А, В... =1,2,3, О ai-SS • "А^= 1,2,3, где а,/?... - векторные индексы, а Л, В... обозначают номер вектора, можно записать соотношения (1.10) и (1.11) в виде de\ = dx^, А-„ rfx^n -ir-"^^- de^ = dx^,. (1.13) (1.14) Умножая равенство (1.13) на е^ и используя условия ортогональ- ности (1.12), получим ЛЛ = ^de\. (1.15) Дифференцируя условия ортогональности (1.12), получим e^tle/n + Cjurfe'*, = 0, dXa/i + d-nns = 0. откуда Следовательно, dx^o = -dXtX.- • (u6) Величины (1.16) описывают бесконечно малый поворот трехмер- ной системы отсчета и определяют трехмерную метрику Киплинга^ Картана dv^dx^dx'». (!-") заданную на группе трехмерных вращении 0(3), действующей на множестве координат yi, у>2, Уз • Умножая^.^иае", и используя условия ортогональнос-и (1.12), получим <'Л_^^_,.р = t^ == е dt--* dt причем тензор угловой скорости вращения системы отсчета связан с компонентами вектора w = dy/df : образом (О ~шз Ш^ = -Шра = - "3 О -^2 ^1 Запишем теперь равенство (1.15) в виде (^1>^2,^з) следующим (1.18) из -Ш1 О QgA dXfc, = i!md<:\ = eAa--^dx' ox' (1.19) и введем обозначение о-Л Т0 - р^р 1 Яч - с л е i7= -4 /?Л 1 (1.20) В результате мы получим локальную связь между дифференциа- лами координат базового пространства dx" и дифференциалами ко- ординат касательного аффинного пространства d\^y в виде dx'-f^T^dx-' , (1.21) где величины Т"» представляют собой локальную связность аффин- ного пространства и называются коэффициентами вращения Риччи. Локальный метрический тензор базы, заданный на множестве трансляционных координат ж", определяется через репер е°д с по- мощью соотношения W=^=^o^=(l,lJ» , при этом риманова метрика запишется как dl2 = ^d^dx» = (dx1)2 + (rf;c2)2 4- (dx3)2 (1.22) (1.23) Таким образом, пространство событий классической механики, учитывающей поступательные и вращательные степени свободы про- извольно ускоренной трехмерной системы отсчета, имеет две метри- ки: Киллинга-Картана (1.17) и Римана (1.23). Эти метрики отражают существование соответственно вращательной и поступательной отно- сительности для уравнения движения (1.5) и (1.6). Запишем теперь Т°д в "координатах слоя" с помощью преобразо- вания Т^-Л^^в- (1-24) По индексам слоя А, В ... величины (1.24) имеют нетензорный за/- кон преобразования ТА' _ kA'-r-A *В , мАлА 1 В'ч - л А1 Ву^ В' + л Л" Д',7 (1.25) где матрицы Л-^ образуют группу вращении 0(3) л^ ё 0(3). (1.26) Используя правило перехода (1.24), запишем равенство (1-21) в локальных индексах Л, В ... dxлв=Tлg^ . (1.27) Разделив это соотношение на dt, получим трехмерную угловую скорость вращения системы отсчетаы^ , записанную в "координатах слоя" • J > •* (1.28) Поскольку в этом соотношении величину Т^ можно обратить в нуль с помощью преобразований в группе 0(3), то и угловая скорость (*?^g является величиной относительной. Заметим, что соотношение (1.28) устанавливает связь между по- ступательной скоростью v'1 == dx"'/dt начала О и угловой скоростью ш^ произвольно ускоренной системы отсчета. Эту связь обеспечи- вает величина Т^ , которая интерпретируется как поле инерции [9]. 1.4. Ограниченность специального принци- па относительности в электродинами- ке В современной физике электродинамика считается наиболее раз- работанной теорией, которая представляет образец для построения других теорий поля. Однако еще Паули заметил, чтэ уравнения Максвелла "...строго справедливы только для равномерно движу- щихся тел и степень их точности, вообще говоря, теи больше, чем меньше ускорение материи [23]". Ограничение на ускорение движу- щихся за, чдов приводит к ограничению примени» ости специального принципа относительности в электродинамике [5 17]. Наибол е просто доказательство ограниченности специального принципа относительности проведено в работе А. Эйнштейна "К электродинамике движущихся тел" [24]. Здесь А. Эйнштейн показы- вает, что специальный принцип справедлив 'только при медлен- ном ускорения заряженных частиц. Утверждение, что четырехмерная формулировка уравнений элек- тродинамики, данная впоследствии Г. Минковским, снимает требо- вание медленного ускорения зарядов при доказательстве ковариант- ности ее уравнений, несостоятельно. Это мы и покажем ниже. Ввиду важности поднятой проблемы и из-за, отсутствия в совре- менной научной литературе работ в атом направлении приведем по- дробно основные положения теоремы Эйнштейна-Пуанкаре, в кото- рой требование малости ускорения выступает основным пунктом при доказательстве ковариантности уравнений электродинамики. Доказательство релятивистской ковариантности уравнений дви- жения ^ = -L-F"-^ (129) * ч ~ ч± .» \i-f-ff ds^ me2 dso невозможно провести без дополнительного условия u, = v = cmst , (1.30) означающего, что скорость движения заряда и» вдоль оси Х равна скорости v инерцмальной системы отсчета, т.е. постоянна. Дей- ствительно, плотность заряда р^ в некоторой инерциальной системе отсчета 5 связана с плотностью ^ в системе отсчета S* , движущейся относительной с постоянной скоростью ч, следующим образом [24] Р;=<>.(1-^ , (1.31) с где и, - скорость заряда в системе S и ^=---== (1.32) /I V3 v'"^ - релятивистский множитель. Инвариантность заряда е в системах S п Sf е' = е = inv (1.33) выполняется при условии, когда плотность наряженной материи пре- образуется согласно соотношению [3] P;=/WT1- (1.&4) Эта формула совпадает с равенством (1.31) лишь тогда, когда спра- ведливо соотношение (1.30). Иными словами, инвариантность заряда (1.33) существует только при движении зарядов с постоянной скоро- стью. Пусть в системе отсчета S заряд е с массой покоя m движется согласно уравнениям m-^=e?,, m-^=e?y, »^=e?.-, (1-35) Перейдем в систему отсчета S' , которая движется со скоростью v = cmst вдоль оси X. Полагая, что в системе S' уравнения (1.35) не меняют своего вида, запишем m''^=e'E'^^ m'd:^^=e'E',- m'^^e'E'•• ^ Вычислим в втих уравнениях производные dx' dy' dz' fx' dy d2г' df ' df ' dt' ' dV ' dt'2 ' dy'2 ' используя преобразования Лоренца x' = (х - vt)f) , j/=y, z'=z, i'=(t-^). (1.37) с Вычисляя компоненты скорости заряда в системе S' , имеем ' - И»-" I _ "» , _ "« "' ~ 1 - U.V/C2 ' "» - 0(1 - U,V/C2) ' "» - /?(1 - Ч^/с-2) • Соответственно, для компонент ускорения находим [24] iPx' _du; _\ u,(\ - u,v/c2) + (и. - v)v,v/c2 df' ~ dt' 0 (1-ч,р/с2)3 ' ' ' fPy' _du', _1 u,,(l-ы,^)/c2)+u^,й„^l/cг dt1'' ~ dt1 0 (1 - u.ti/c2)3 ' ' ' iPz' _du', _ I u,(l - u,v/c2) + u,u.v/c2 dt1'' dt' 0 (1-u.c/c2)3 ' ••1ли' где ч» = duz/dt i и, = duyldt , и, = du,/dt . (1-41) Пусть теперь в системе отсчета S1 заряд "мгновенно покоится" [24], тогда выполняются соотношения и, = 0 , и, = в = cons* , е' = е = inv , m' = m , (1.42) где m - масса покоя заряда. Поскольку движение идет только вдоль оси X, то составляющие скорости вдоль осей Y и Z равны нулю и, = и. = 0. (1.43) Выражение "мгновенно покоится" означает, что система отсчета 5" связана в данный момент с самим зарядом. Лля заряда, движуще- гося прямолинейно и равномерно, система S1 является системой от- счета, в коте{юй он "мгновенно покоится" во всех точках траектории. Поэтому для рассматриваемой ситуации, когда выполняются усло- вия (1.42, 1.43), обращаются в нуль как производные (1.38)-(1.40), так и производные (1.41), поскольку заряд движется относительно системы S прямолинейно и равномерно со скоростью Us = v == const. Очевидно, что прямолинейное и равномерное движение зарядов про- исходит в отсутствие внешних полей, поэтому уравнения движения (1-36) строго ковариантны относительно преобразований Лоренца (1.37) только для свободных зарядов- Предположим теперь, что заряд движется, согласно уравнениям (1.36), с малым ускорением, вызываемым внешним полем Е- Теперь условия (1.42) выполняются лишь приближенно 1*д ^ 0 , их ^ v •= const , е' = е == inv , m' •= т . (1-44) Используя первые два условия (1.44), можно записать производные (1.38-1.40) в виде s^s-^ ^ ё-^ ^ ^ /,2^ ^=/?^- (1-40 Перлое из этих соотношений доказывается следующим образом. Из условия Молости ускорения Ur(<) ^ v = const вместо (1,:}'2) можн< записать ^ = -- ^ const , (1.48) ^1 -"КОЛ2 поэтому ^{и^} = /Зи, + и,/3 = /?и, + ^и,4 == ^ f^+^= ^"д • Qv С \ С ^J / Здесь было использовано соотношение ^+-"l~i ^+0)-1' которое следует из (1.48). Подставляя (1.45)-(1,47) в уравнения (1.35) и учитывая соотношения (1.44), а также преобразование полей ^ = Е, , ?, = (Е, - "Н,)/3 . Е', = {Е, + '-Н,)0 , Н, = И. , Н' = (Я, + "-Е.}Р , Я; = (Н. - "Д,)/? , • С С запишем уравнения (1.35) в виде т^-^ = ^(""^ = еЕХ ' (1-49) m^=^(mu^)=e(^-^)) ^^ = ^("i"^) = е(^ + ^) . Поскольку г ^ ид и Uy =: Us = О, то мы можеу переписать уравне- ния (1.49) как -(mu,/3) = е(^ + ^Я. - ^Яу) , (1.50) ui с с -'(ти,/Э) = е(Е, + ^Н. - "^Я,) , ut С С ^(mu^) = е(Д, + "?ff, - "S-H.) . ai с с Далее, следуя M. Минковскому, можно записать уравнения (1.50) в четырехмерном виде. Для этого введем четырехмерное псевдоевкли- дово пространство Минковского с интервалом ^^-^[Ф^Ф2^)2]}^ (1.51) / 2\ 1/2 ^(l-^) , четырехмерный вектор скорости и' с компонентами u'=(/?,^), a =1.2,3 (1.52) и четырехмерный тензор электромагнитного поля F^ с компонента- ми / 0 -Ег -Еу -Е, \ Используя соотношения (1.51)-(1.53), перепишем уравнения (1.50) следующим образом: d Добавляя к уравнениям (1.54) уравнение для мощности электриче- ских сил, которое через величины (1.51)-(1.53) запишется как d dso получим уравнения движения классической электродинамики (1.29), записанные в четырехмерном виде. 1.5. Пределы применимости специального принципа относительности в электро- динамике Совершенно очевидно, что четырехмерная запись уравнений дви- жения ничего не изменила относительно условия малости ускорения заряда. Более того, можно утверждать, что без этого условия четы- рехмерная запись уравнений электродинамики в ковариантном от- носительно преобразований Лоренца виде вообще невозможна. Со- временные теоретики забыли об атом весьма важном обстоятельстве. Величину внешних полей, для которых справедлив специальный принцип относительности в электродинамике Максвелла-Лоренца, можно определить следующим образом. Умножим уравнения движения (1.29) на Ге = ^/тс3 - классиче- ский радиус электрона (характерный параметр классической элек- тродинамики) '> •Ч • -Я J_ е2 rf2»' e Условие малости ускорения означает, что безразмерное ускоре- ние в левой части этих уравнений мало, откуда следует Ускорение, удовлетворяющее неравенству (1-55), как раз и опре- деляет границы применимости специального принципа относительно- сти в электродинамике. В структурном виде неравенство (1.55) можно записать как Из этого неравенства следует, что специальный принцип относи- тельности в электродинамике нарушается: в больших по величине электромагнитных полях и при ультрарелятивистских скоростях за- ряженных частиц. При не релятивистских скоростях из (1.56) следует и<"^. Подставляя сюда заряд и массу электрона, имеем следующую оценку для сильных электромагнитных полей Электромагнитные поля, удовлетворяющие неравенству (1,57) явля- ются слабыми и для малых времен наблюдения специальный принцип относительности для таких полей выполняется с достаточной степе- нью точности. Для заряда, равному заряду электрона, пиля Е и Н появляются на расстояниях см (1.58) Сделанные нами выводы оказываются справедливыми как для классической, так и для квантовой электродинамик- Вот что гово- рит П. Дирак о границах применимости квантовой электродинами- ки: "Существующая квантовая теория хороша до тех пор, пока мы не пытаемся распространить ее слишком далеко, а именно, когда мы не пытаемся применить ее к частицам высоких анергий, а также в области малых расстояний [1]". 1.6. Некоторые следствия нарушения спе- циального принципа относительности в электродинамике Условие применимости специального принципа относительности в электродинамике (1.55) накладывает ограничение на допустимые ускорения и скорости зарядов, поэтому, как только мы попытаемся использовать уравнения электродинамики для ситуаций, где нера- венство (1.55) нарушается, возникает целый ряд трудностей. Например, единственная модель заряда, которая следует из ли- нейных уравнений электродинамики, - это модель точечного заряда с плотностью ffe = eS(r) . Электромагнитное поле такого заряда простирается по координате г от 0 до оо, однако уже на расстояния г ^ Ге == 2, 8 • IC^^CM от центра заряда, равного заряду электрона, специальный принцип относитель- ности нарушается. Попытка применить уравнения электродинамики на расстояниях меньше Гс приводит к результатам, противоречащим здравому смыслу. Действительно, вычислим энергию W электроста- тического поля Е заряда, радиус которого равен а W= /I Г00 е2 ^dV=- е-.- 8я- J, г* -4я•r2(^r == е- '2г е" 2а ' (1.59) Для точечного заряда о -•- 0 , поэтому из (1.59) следует W -* оо . По формуле т = W/c2 масса такого заряда бесконечно большая, и, сле- довательно, его невозможно было бы сдвинуть с места. Понятно, что противоречащий здравому смыслу результат получился из-за непра- вомерности применения формулы (1.59) на расстояниях г < г<. Нарушение специального принципа относительности при больших ускорениях заряда (в сильных полях) возникает и при изучении про- блемы излучения ускоренно движущегося заряда. При ускоренном движении заряда в уравнениях движения (1.29) появляется дополни- тельный член, связанный с силой реакции излучения. Эту силу на- ходим из решения уравнений Максвелла 4ЭГ- OAk = -3k , с t, Jb=0.1,2,3 в которых скорость источника переменна. Рассматривая заряд как жесткую сферу радиуса а с равномерным распределением заряда на ней, М. Абрагаам и Г. Лоренц нашли следующие уравнения движе- ния заряда с учетом силы реакции излучения [23] / 2е2 \^ е 2е2 m + --, х == еЕ + - [хН] + -з х +. \ Зое2 У с- 3<~ (1.60) х =: dx dt Остальные невыписанные члены этого уравнения» содержащие че- твертую и т.д. производные х по времени, умножаются на возра- стающие степени радиуса а . В уравнениях (1.60) сила еЕ+^хН] с представляет собой внешнюю силу, под действием которой происхо- дит ускорение заряда, сила 2е2 ... ^х является силой реакции излучения. Дополнительная к массе покоя т электромагнитная масса 6т 2е2 Зас2 для точечной частицы (при а -*• 0) становится бесконечно большой, поэтому никакими разумными внешними силами ускорить такой за- ряд невозможно- Этот результат получается как следствие того, что мы продвинули уравнения электродинамики в область малых рас- стояний, где поля становятся сильными и неравенство (1.55) для них нарушается. Обычно при переходе к точечной частице член, содержащий массу 6т, отбрасывают и записывают уравнения движения излучающего заряда в виде тх == еЕ + ^[хН] + 1-х . (1.61) С Ot/ Этот прием отбрасывания бесконечно больших величин из урав- нений квантовой электродинамики получил название "процедура пе- ренормировки" [25]. Однако прием подобного рода только маскиру- ет существующую в электродинамике проблему - ограниченность специального принципа относительности и, как правило, приводит к другим бессмысленным результатам. Например, при отсутствии внешней силы уравнения (1.61) принимают вид .. 2е2 ... mx=^x . Эти уравнения имеют два решения: а) тривиальное, когда х == 0; б) самоускоряющееся, когда / зе3 .. x=aexp(2m^)• (1.62) где а- ускорение в момент временив = 0. Из решения (1.62) следует, что достаточно самого небольшого начального ускорения а для того, чтобы заряд начал самоускоряться под действием силы реакции из- лучения. Таким образом, в электродинамике существует проблема излучения ускоренного заряда, которая опять-таки связана с огра- ниченностью специального принципа относительности. Это следует из уравнений, которые представляют собой четырехмерную запись уравнений (1.61) ik dxt ->- 1 «• --+ -Я dSQ me где . (1.77) В этих уравнениях величины v , ^ и р определяются как .iS V>=aexp(-), p=,li'^,= Wг=a'' , v m (1.78) Уравнения квантовой жидкости (1.71) и (1.77) отличаются от урав- нений классической жидкости добавочной квантовой потенциальной анергией V up 1 [Vt> (1.79) 2\ Р которая отлична от нуля даже в том случае, когда квантовая частица свободна. Квадтовую жидкость, описываемую уравнениями (1.71) и (1.77), можно рассматривать как возбужденные состояния некоторой упру- гой среды, называемой в квантовой теории поля физическим ваку- умом- Отсюда следует очень важный вывод: - детерминистический подход в квантовой теории возможен в том случае, если мы сможем построить теорию физического вакуума и будем рассматривать ча- стицы различной природы как его возбужденные состояния. К подобным взглядам пришли российские физики Я. Френкель [45] и Л. Блохинцев [4б]. Л- Блохинцев, например, пишет [47]: "Согласно этой точке зрения частицы являются лишь возбуждениями вакуума, который продолжает жить и тогда, когда никаких частиц нет; в нем флуктуирует электромагнитное поле и электрическая поляризация. Это - не покой, а вечное движение, подобно зыби на поверхности моря.. - С этой точки зрения ясно также, что никаких изолирован- ных, предоставленных самим себе ("свободных", как говорят) частиц не существует. Лаже в случае значительного удаления частиц друг от друга, они все же продолжают принадлежать породившей ее сре- де, находящейся в состоянии непрерывного движения. Возможно, что в этой связи частиц и среды и скрывается природа той невозможно- сти изолировать частицу, которая проявляется в аппарате квантовой механики". Фактически Л. Влохинцев заметил, что в квантовой теории, осно- ванной на специальном принципе относительности, предполагающем существование изолированных (движущихся прямолинейно и равно- мерно) частиц, в действительности таковых частиц не существует из-за флюктуаций физического вакуума. Это еще одно из серьезных противоречий квантовой теории, которое А. Эйнштейн пытался пре- одолеть путем построения " разумной общерелятивистской теории" и в рамках ее "более совершенной квантовой теории" [Зб]. 1.9. Феноменологический характер теорий в области микромира Все физические теории можно разделить на три больших клас- са: фундаментальные, феноменологические (или конструктивные) и полуфеноменологические. 1.9.1. Фундаментальные теории Эти теории базируются на физических принципах, имеющих все- общую приложимость (конечно, в тех рамках, в которых эти прин- ципы справедливы). Уравнения фундаментальных теорий обладают "абсолютной" предсказуемостью, т.е. теоретические предсказания явлений, сделанные на основании точных решений фундаментальных уравнений, полностью подтверждаются экспериментальными факта- ми. Это свойство фундаментальных уравнений делает их бесценным и наиболее совершенным орудием исследования природы. Обобщение фундаментальных теорий - стратегическая зада- ча теоретической физики - представляет собой наиболее трудоем- кую работу для физика-теоретика. Физиков, которые создавали или обобщали уже существующие фундаментальные физические теории, можно пересчитать по пальцам. Примером фундаментальных физи- ческих теорий являются: теория гравитации Ньютона, электродина- мика Максвелла-Лоренца, теория гравитации Эйнштейна и т.д. Здесь мы перечислили теории, которые позволяют описывать гра- витационные и электромагнитные взаимодействия фундаментальным образом. Действительно, точные решения уравнений только этих те- орий приводят к потенциалам взаимодействия масс и зарядов (потен- циал Ньютона, потенциал Кулона, потенциал Эйнштейна для реше- ния Шварцшильда уравнений эйнштейновской теории гравитации). Все другие взаимодействия (сильные и слабые), обнаруженные экс- периментально как отклонения от законов фундаментальных теорий, имеют феноменологическое или полуфеноменологическое описание. 1.9*2. Феноменологические теории В отличие от фундаментальных, в которых используется аналитиче- ский метод, феноменологические теории используют метод синтети- ческий . Эти теории возникают в физике "под давлением эксперимен- тальных фактов" и представляют собой скорее метод для системати- зации данных опыта в тех областях физики, где фундаментальные теории еще не созданы. Потенциалы взаимодействия в феноменологических теориях под- бираются искусственным образом так, чтобы удовлетворительно описать феноменологические взаимодействия. Как правило, в фено- менологические потенциалы входят одна или несколько подгоночных констант, значения которых определяются путем согласования тео- рии с данными эксперимента. Феноменологические теории облада- ют слабой предсказательной силой (образно говоря, предсказывают на расстоянии вытянутой руки) и не раскрывают истинной природы физического явления. Примером феноменологических теорий явля- ются: теория ядерных сил, теория электромагнитных формфакторов и др. Как известно, ядерные взаимодействия были впервые обнаружены Э. Резерфордом [48] при исследовании упругого рассеяния ст-частиц (ядер гелия) в кулоновском поле ядер тяжелых элементов. Ученому удалось показать, что на расстояниях r "S> 10~12 - 10~13 см от центра ядра взаимодействие й-частиц и ядер описывается фундаментальным потенциалом Кулона. Однако на расстояниях порядка 10~12 - 10~13 см от центра ядра было обнаружено отклонение от фундаментального кулоновского рассеяния. Для феноменологического описания этого отклонения Э. Резер- форд ввел понятие гипотетических ядерных сил, действующих на малых расстояниях от ядра. Поскольку в то время (и по сей день) не существовало фундаментальных уравнений для описания ядерных сил 1 , то пришлось вводить феноменологические потенциалы, по- зволяющие хоть как-то описать и систематизировать ядерные вза- имодействия. В ядерной физике существует несколько типов таких потенциалов. Приведем некоторые из них [49-51]. Сферически симметричная прямоугольная яма конечной глубины У(г}=[ -Va , r <, R О , г>Д (1.80) Экспоненциальный потенциал (1.81) н Потенциал Хюльтена V(r)= •Va ехр(- к l-exp(-g) (1.82) lИзвecтнoe решение уравнения Юк&вы [4Э], приводящее к короткодейству- ющему потенциалу взаимодействия, не описывает всего многообразия свойств ядерных сил. Потенциал Вудса-Саксона V(r) == -Vo Оптический потенциал U У(г) = iW (1.83) (1.84) Все параметры, входящие в потенциалы (1.80-1.84) определяются с помощью подгонки к экспериментальным данным. Они не являют- ся константами, а варьируются в зависимости от внешних условий ( энергии частицы» зарядового и массового чисел ядер и т.д.) Есте- ственно, что наилучшим образом воспроизводит экспериментальные данные потенциал, имеющий наибольшее число подгоночных параме- тров ( в данном случае оптический потенциал, имеющий шесть пара- метров ). Подобно ядерным взаимодействиям, феноменологическая теория электромагнитных формфакторов была построена после того, как Е- Кизингер [52], Р- Хофштадтер и др. [53, 54] обнаружили отклонение от кулоиовского взаимодействия при упругом рассеянии электронов на ядрах (отклонение от формулы Мотта [55]). Р. Хофщтадтер [53] предложил смоделировать аномальное рассея- ние электронов с помощью введения некоторого феноменологическо- го распределения заряда ядра, отличного от точечного. Таким обра- зом, рассеяние электронов стало зависеть от формы распределения заряда в ядре. Явный вид распределения зарядов вводится в теорию искусственно, поскольку не существует каких-либо фундаментальных уравнений, из которых его можно получить. Приведем некоторые распределения заряда, используемые в тео- рии электромагнитных формфакторов [56]. Однородное ро , r < a О , г> а Гауссовское (1.85) /?(г)=/>оехр(-^) . (1.86) Экспоненциальное /?(г)=/»оехр(--) . (1.87) Модифицированное экспоненциальное • ^. ^ »р(-) р[г) = ра Вудса-Саксона (1.88) Ра (1.89) Однопараметрические распределения заряда (1-85-1.89) приме- няются в основном для легких ядер. Для средних и тяжелых ядер применяются двухпараметрические (1.89) и более сложные распре- деления заряда- Параметры распределений (1.85-1.89) не являются раз и навсегда установленными константами для одного сорта ядер, а зависят от внешних условий, например от диапазона энергии рас- сеиваемых электронов. 1.9.3. Полуфеноменологические теории Существующие теории элементарных частиц носят полуфеномено- логический характер. В основе такой теории лежит фундаменталь- ная теория, усложненная добавочными предположениями феномено- логического характера. Наиболее яркий пример полуфеноменологической теории - тео- рия электрослабых взаимодействий Вайнберга-Салама-Глашоу [57- 60]. Создание феноменологических и полуфеноменологических теорий - оперативная задача теоретической физики. Подобные теории представляют собой всего лишь промежуточный этап при создании фундаментальной теории и основная цель теоретической физики со- стоит в замене феноменологических и полуфеноменологических тео- рий фундаментальными теориями. Надо отметить, что А. Эйнштейн никогда не занимался теорией ядерных сил, электромагнитных формфакторов или какой-либо дру- гой феноменологической теорией. Для себя он считал эту работу бесполезной, полагая, что ". ..теории, которые постепенно приспоса- бливаются к наблюдаемым данным, приводят к страшному накопле- нию разрозненных утверждений" [61]. Опасения А. Эйнштейна не были напрасными, поскольку совре- менные теории объединительного характера представляют собой пе- струю картину многих аналитически несвязанных явлений. Идет процесс дезинтеграции науки и теоретикам приходится больше запо- минать, чем понимать физические явления. Дело дошло до того, что теоретикам приходится составлять словари для объяснения многих понятий и явлений в области микромира, чтобы понять друг друга. Подойти к построению фундаментальной теории явлений в обла- сти микромира А. Эйнштейн предполагал следующим образом. В левой части его знаменитых уравнений 8тг<7 -т- ^ }гп стоит чисто геометрическая величина (тензор Эйнштейна Gjm = Rjm - -QjmR}, а справа феноменологический, вообще говоря, "вве- денный руками", тензор энергии-импульса материи Tjm . Таким образом, в теории А. Эйнштейна материя выступает на фоне искри- вленного пространства-времени как самостоятельная, независимая от пространства-времени сущность. Феноменологическое представление тензора Tjm не устраивало А. Эйнштейна [62] поскольку: "Правая часть включает в себя все то, что не может быть пока объединено в единой теории поля- Конеч- но, я ни одной минуты не сомневался в тон, что такая формулировка есть только временный выход из положения, предпринятый с целью дать общему принципу относительности какое-то замкнутое выраже- ние. Эта формулировка была ведь по-существу не более чем теорией поля тяготения, несколько искусственно оторванного от единого поля пока еще неизвестной природы." Способ, с помощью которого можно избавиться от произвола при выборе тензора энергии-импульса, А. Эйнштейн видел в геометри- зации тензора энергии-импульса материи, стоящего в правой части уравнений Эйнштейна (1.90). По мнению ученого, геометризация тен- зора энергии-импульса материи должна привести к гео метризации полей материи, образующих его. Для А. Эйнштейна геометризация полей материи означала построение фундаментальной теории явле- ний в области микромира, согласованной с принципом относительно- сти. 1.10. Геометризация физики и проблема ва- куума Мысль о том, что великая пустота (или вакуум) есть источник окру- жающего нас мира, уходит вглубь веков. Согласно представлениям древних философов Востока все материальные объекты возникают из великой пустоты, являются ее частью и в этом смысле иллюзорны. В самой великой пустоте постоянно совершаются акты творения реаль- ных объектов. Например, вот как описан диалог о великой пустоте (1.90) между учителем и учеником (ученик задает вопрос) в древнеиндий- ских ведах [63]: "Каков источник этого мира? - Пространство, - ответил тот. - Поистине все эти существа выходят из простран- ства и возвращаются в пространство, ибо пространство больше их, пространство - последнее их прибежище". Подобные взгляды на пространство у европейцев возникли перед созданием механики Ньютона. В конце XVI в. итальянский философ Ф. Патриции по этому поводу писал следующее [64]: "Итак простран- ство есть то, что было прежде мира и будет после него, что стоит во главе мира, из него исходит и, наконец, обращается в нечто... Разве оно тогда не является субстанцией? Если субстанция то, что лежит в основе, то пространство и есть скорее всего сущность". Современная физика, начало которой положила механика Ньюто- на, развивалась как теория измерения расстояний и моментов време- ни движущихся относительно инерциальных систем отсчета матери- альных тел. Полученное в результате измерений множество коорди- нат и времени подвергалось обработке, после чего строились сперва уравнения траекторий, а затем и уравнения движения в дифференци- альной форме. Эта связь между геометрией пространства событий и механикой была замечена уже И. Ньютоном [б5], который писал: "Геометрия основывается на механической практике и егть не что иное, как та часть общей механики, в которой излагается и доказы- вается искусство точного измерения". Так же как и евклидова геометрия механики Ньютона, геометрия искривленных пространств, созданная Н. Лобачевским [66] и Б. Ри- маном, в своей основе содержат физический опыт измерения. В рабо- те "О гипотезах, лежащих в основании геометрии" Б. Риман отмечал [67]; "предложения геометрии не выводятся из общих свойств протя- женных величин, напротив, те свойства, которые выделяют простран- ство из других мыслимых трижды протяженных величин, могут быть почерпнуты не иначе, как из опыта". Еще большее сближение представлений восточных и европейских ученых мы находим в точке зрения на природу материи английского математика В. Клиффорда, который в философской статье "О про- странственной теории материи" [68] прямо говорил, что: "в физи- ческом мире не происходит ничего, кроме изменения кривизны про- странства, подчиняющегося (возможно) закону непрерывности". Согласно В. Клиффорду материя представляет собой сгустки про- странства, своеобразные холмы кривизны на фоне плоского про- странства. Идеи В, Клиффорда нашли свое развитие в работах А. Эйнштей- на, которому удалось представить гравитационное поле через кри- визну четырехмерного пространства-времени. Пустое, но'искривлен- ное пространство в теории Эйнштейна удовлетворяет вакуумным уравнениям Rik^Q, (1.91) решение Шварцшильда [69] которых находит подтверждение на опыте (смещение перигелия Меркурия, отклонение луча света в поле Солн- ца, запаздывание радиосигналов в гравитационном поле и т.д.). Заметим, что вакуумные уравнения Эйнштейна не содержат ни- каких физических констант . Они являются чисто полевыми не- линейными уравнениями и А. Эйнштейн считал, что правильное об- общение именно этих уравнений приведет нас к уравнениям единой теории поля- Он писал [70]: "Я считаю, далее, что уравнения грави- тации для пустого пространства представляют собой единственный рационально обоснованный случай теории поля, который может пре- тендовать на строгость (с учетом так же нелинейных членов). Все это приводит к попытке обобщения теории гравитации для пустого пространства". Опираясь на работу Райнича [71], ученик А. Эйнштейна Дж. Уи- лер предложил рассматривать уравнения Эйнштейна, в правой части которых стоит тензор энергии-импульса электромагнитного поля Rik - ^QikR (1.92) SWG Г 1 /г rm 1- г г^р-il •~?~ [^(FirnF k ~ -^^ ')J как уравнения "исконно единой теории поля" [72]. Однако отметим» что эти уравнения были известны А. Эйнштейну [73] и он не считал их уравнениями единой теории поля, поскольку: правая часть этих уравнений отлична от нуля в пределе Rue = R = 0, а левая обращает- ся в нуль; неизвестно каким образом в данном случае описываются частицы материи спина 1/2, например электроны, создающие элек- тромагнитные поля. Трудности в геометрическом описании спинорных полей, по мне- нию самого Дж. Уилера [72], состоит в том, что: "мысль о получении понятия спина из одной лишь классической геометрии представля- ется столь же невозможной, как и потерявшая смысл надежда неко- торых исследователей прежних лет вывести квантовую механику из теории относительности". Дж. Уилер произнес эти слова в I960 г. во время чтения лекций в Международной школе физики им. Э. Ферми. Тогда он не знал, что уже начал свои блестящие работы Р. Пенроуз [74, 75], который показал, что-именно спиноры могут быть положены в основу клас- сической геометрии и что именно они определяют топологические и геометрические свойства пространства-времени, например, как его размерность и сигнатуру. Р. Пенроуз записал вакуумные уравнения Эйнштейна (1.91) в спи- норном виде [74] ^ABCD = ° А,В...=0,\ , С,Д...==0,1 (1.93) и совместно с Э. Ньюменом предложил систему нелинейных спинор- ных уравнений [76] °) дABfficD~дCD(гiAB=?PQ{TPACDff^QB~ ^PCAB^QD^^^RBDC^AS ^^DBA^CS^ ' Ь) ^ACDF^EB -+- ^ACBE^fD -+- ^?gg{?CD?AF + SAD^CF)- ^DI^ACFE + дf'ET^DB+? (TAPDBTQCFE+ ^ACPB^QDFE ~^APFE^QCDB ^ACPE^QFDB^ 'ACPB^QDFE '^ACFft-'SEBD I 1-Д5/Т •Т- - • "T6 ^ACDR^SBEF (1.94) с) д^лврс - ^AB)bx - ^РШ.лвТ^- -^SABCPT^ ^ +2TP^Фc)PXD- т- • - <ь xv -t v Ф х • = Q ~lXDV(AчfBC} ^х V{A BC)D •' ' (Ф ^ Р1 •А Х VW/ф Х . 'т, . .Р, I- л 0 IV 4W ' АРВХ ' ^ АР W BXV. 4.Д •*'Т .'•14-» ХтРЯ.Л.ф XJ-РЙ. .^0 +*0,f- -=0,1 , y,/l,l/.-==6,i , обобщающей нелинейные спинорные уравнения Гайзенберга-Иванен- ко (1.103). +' +' Спинорная запись уравнений физического вакуума (А ) и {В ) со- впадает с матричными уравнениями Кармели (1.97а) и (1.97Ь) и экви- валентна спинориым уравнениям [1.&4а) и (1.94Ь). Это означает, что Э. Ньюмен, Р. Пенроуз и М- Кармели (при использовании уравне- ний формализма Ньюмена-Пенроуза) вышли за рамки традиционной геометрии Римана, лежащей в основе теории гравитации Эйнштей- на и фактически имели дело со структурными уравнениям Картана геометрии абсолютного параллелизма [21]- С точки зрения теоретической физики такой шаг не может трак- товаться чисто формально и требует весомых физических обосно- ваний. Всеобщий принцип относительности позволяет сделать это. Более того, этот принцип утверждает, что уравнения формализ- ма Ньюмена-Пенроуза можно рассматривать как новые физические уравнения. Таким образом, теория физического вакуума, основанная на все- общем принципе относительности предлагает реализацию програм- мы Клиффорда-Римана-ЭйнштеЙна-Пенроуза-Гайзенберга в рамках геометрии абсолютного параллелизма со спинорной структурой. При этом структурные уравнения геометрии абсолютного парал- лелизма [А) и (В) объявляются уравнениями физического вакуума. Эти уравнения обладают тремя особенностями, которые отличают их от всех существовавших до сих пор физических уравнений. Во- первых, они не содержат никаких физических констант, во-вторых, их решения скорее конструируются, чем находятся (см. Часть 2) и ^наконец, все входящие в них величины носят относительный ха- рактер. Перечисленные свойства уравнений вакуума потребуют от исследователей использования новой научной методологии. Глава 2 Физические принципы и уравнения теории физического вакуума 2.1. Принцип всеобщей относительности и основные физические идеи, ведущие к нему "Все в мире относительно," - этот известный философский те- зис А. Эйнштейна как нельзя лучше подтверждает развитие физики; сперва на основании опыта некоторая физическая величина посту- лируется как абсолютная, однако позже (по мере накопления новых экспериментальных данных) вдруг обнаруживается, что она относи- тельна. Во вр-. мена Аристотеля предполагали, что си тема отсчета, свя- занная с Землей находится в абсолютном покое но затем Галилей (опираясь . а данные опыта) показал, что покой и равномерное пря- молинейно" движение относительны- Чтобы дать научное обоснование покою и равномерному прямоли- нейному движению, Ньютон вводит гипотетическое абсолютное про- странство. Кроме того, опыты в механике и других разделах физики показывали, что время, масса, тел, силы, (исключая силы инерции) являются абсолютными величинами- Такие представления сохранялись в физике до тех пор пока не на- чались эксперименты с объектами, которые движутся со скоростью

Сайт создан в системе uCoz